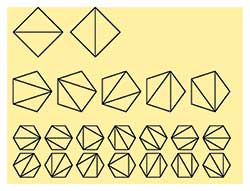
Рассмотрим правильные многоугольники и для каждого из них рассмотрим число способоа разрезать его непересекающимися диагоналями на треугольники. . Треугольник пропустим: он не имеет диагоналей, но 1 способ его получения есть. Для четырехугольника - два варианта , пятиугольник можно разрезать диагоналями пятью способами, а шестиугольник 14. Рассечение некой плоской фигуры на треугольники называется триангуляцией. Триангуляция семиугольника непересекающимися диагоналями может быть осуществлена 42 способами, а восьмиугольника -.132. Получена последовательность чисел: 0 1 2 5 14 42 132.... , названная в честь белгийского матаматика Эжена Каталана - «последовательность Каталана»

Эта последовательность встречается при решении разнообразных задач. Например, взяв пару скобок (открывающую и закрывающую) можно получить только одну скобочную последовательность ( ). Две пары скобок: lдают две последовательности (( ) ) ( )( ). Три пары скобобок ((())) ()()() (())() ()(()) (()()). пять скобочных последовательностей. Опять получаем числа Каталана. Последовательность подчиняется рекурентному соотношению:

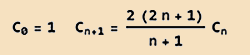
В рекурентном соотношении каждое следующее значение вычисляется с использовании предыдущего.

Задача - усложненный вариант задачи «Задача Я.И. Перельмана I »

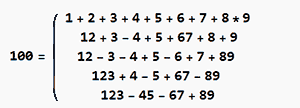
Из цифр 123456789 путем объединения некоторых из них без нарушения порядка, расставляя знаки арифметических операций (+,-,*,/), и скобки (соблюдая баланс ) получить заданное число..

Задачу решать с учетом минуса перед числом и без него.

за счет введения скобок, что требует соблюдения бпланса этих скобок и решения проблемы при возможной попытке деления на 0.

Ответить на вопрос: cколько вариантов решения данной задачи

В заданном интервале чисел найти числа, которые нельзя представить данным способом

Новизна — применение Wolfram Mathematica.

Алгоритм:

Переведем число 123456789 в строку символов, далее строку переведем в одномерный массив символов, создадим строку символов арифметических операций с добавлением символа "_" - объединение соседних цифр, т.е. "+-*/_",
Скобка может быть -открыывающая перед числом, перед другой скобкой, после знака операции или после другой скобки. Скобка закрывающая после числа или скобки, перед другой скобкой, перед знаком операции или знаком конца выражения.
После знака деления необходима проверка скобочного выражения на 0 переведем и эту строку в одномерный массив символов.
В исходном числе 123456789 иммется 8 промежутков между цифрами. Wolfram Mathematica позволяет сгенерировать 8⁵ комбинаций всех возможных операций (Tuples). К нашему счастью в исходном числе отсутствует 0 - не надо проверять деление на 0.
Для каждой комбинации операций последовательно переписываем симолы-цифры исходного числа и знаки операций между ними, если это не "_". Полученную строку переводим в выражение (ToExpression) и проверяем его равенство заданному числу. Все.


SetAttributes[f, {Flat, OneIdentity}]
e : CirclePlus[___, _List, ___] := Distribute[Unevaluated[e], List]

tt = Tuples[{"#", "-"}, 8]; sum = 0;

ss = Characters["123456789"]; vv = {};
Button[" ", Print[ww, "   ", sum, "  ", i, "  ", sd]]
For[i = 1, i <= Length[tt], i++,  (*256*)
  sd = StringDrop[
    StringDrop[
     StringReplace[
      ToString[ Riffle[ss, tt[[i]]]], {"," -> "", "#" -> ",", 
       "-" -> "", " " -> ""}], 1], -1];
  
  
  st = ToExpression[
      "f[" <> Characters /@ sd <> "]"] //. {f[x__] :> 
       ReplaceList[f[x], f[u_, v_] :> CirclePlus[u, v]]} // Flatten;
  st = ToString /@ st;
  
  lst = Length[st]; (* 1430 *)
  ff = Characters[First[st]];
  cc = Count[ff, ⊕];      op = Tuples[{"+", "-", "*", "/"}, cc];
  lop = Length[op];  Print[lop];
  For[j = lst, j >= 1, j--,
   yu = Select[Characters[st[[j]]], # != " " &];
   For[n = 1, n <= lop, n++,  
    yy = yu;
    xx = op[[n]]; k = 1;
    For[m = 1, m <= Length[yy], m++,
     If[yy[[m]] ==⊕, yy[[m]] = xx[[k]]; k++]];
    zz = StringJoin[yy]; aax = Quiet[ToExpression[zz, StandardForm]];
    
    If[aax == 100, ww = zz; Print[zz, "=100"]; sum++]]]];

В итоге 100

(((((1(2+3))(4*5))+6)-7)-8)+9	==100
(((((1(2+3))(4*5))-6)+7)+8)-9	==100
(((((1(23))+(4+5))*6)-7)+8)+9	==100
(((((1(2/3))+(45))*6)-7)-8)-9	==100
(((((1(2/3))/(4+5))6)7)+8)9	==100
(((((1+2)+((3+4)+5))*6)-7)+8)+9	==100
(((((12)((3+4)*5))+6)+7)+8)+9	==100
(((((1+2)+(3+(4+5)))*6)-7)+8)+9	==100
(((((1+2)-(3/(4+5)))/6)7)+8)9	==100
(((((12)/(3(4+5)))6)7)+8)*9	==100
((((1+(((2+3)+4)+5))*6)-7)+8)+9	==100
((((1+(((2/3)-4)+5))/6)7)+8)9	==100
((((1+((23)-4))(5*6))-7)+8)+9	==100
((((1+((2/3)4))(5*6))+7)-8)-9	==100
((((1((2-3)+4))(5*6))-7)+8)+9	==100
((((1((23)+4))*(5+6))+7)-8)-9	==100
((((1+(2+(3+4)))*(5+6))+7)-8)-9	==100
((((1+(2/(3+4)))(5+6))7)-8)+9	==100
((((1+(2/(3/4)))(56))+7)-8)-9	==100
((((1-(2(3-4)))(5*6))-7)+8)+9	==100
((((1-(2/(3-4)))(56))-7)+8)+9	==100
((((1(2-(3-4)))(5*6))-7)+8)+9	==100

(1+(2((3((45)-(6-7)))8)))-9	=1000
(1+(2(((3(4+5))+6)*(7+8))))+9	=1000
(1-(2(((3/(4-5))-6)(7*8))))-9	=1000
(1-(2(((3(4-5))-6)(78))))-9	=1000
(1+(2((3-((4-5)6))(78))))-9	=1000
(1+(2((3((4+5)-6))(78))))-9	=1000
(1+(2((3(4+(5-6)))(78))))-9	=1000
(1+(2(3((((4+5)-6)7)8))))-9	=1000
(1+(2(3((((45)-6)+7)8))))-9	=1000
(1+(2(3(((4+(5-6))7)8))))-9	=1000
(1+(2(3(((45)-(6-7))8))))-9	=1000
(1+(2(3(((4+5)-6)(78)))))-9	=1000
(1+(2(3((4+(5-6))(78)))))-9	=1000
(((1+((2-3)/(4+5)))+6)+7)(89)	=1000
(((((1+2)3)+4)(5+6))*7)+(8-9)	=1000
((1+(((2-3)/(4+5))+6))+7)(89)	=1000
(1((2+3)(4((56)*(7+8)))))/9	=1000
(1((2+3)(4(5(6*(7+8))))))/9	=1000
(1-(2((((3/(4-5))-6)7)*8)))-9	=1000
(1-(2((((3(4-5))-6)7)8)))-9	=1000
(1+(2(((3-((4-5)6))7)8)))-9	=1000
(1+(2(((3((4+5)-6))7)8)))-9	=1000
(1-(2+(((3-((45)6))-7)*8)))+9	=1000
(1+(2(((3(4+(5-6)))7)8)))-9	=1000
(1-(2+(((3-(4(56)))-7)*8)))+9	=1000

Получить в итоге 1000 -

Перельман Я.И. Занимательная арифметика. Издание 1-е. Ленинград, "Время", 1926 — 192 c.
https://habrahabr.ru/post/115066/
http://math.all-tests.ru/taxonomy/term/9?page=1
https://habrahabr.ru/post/312920/
https://pro-prof.com/archives/578 скобки

Задача Я.И.Перельмана-II

Алгоритм: