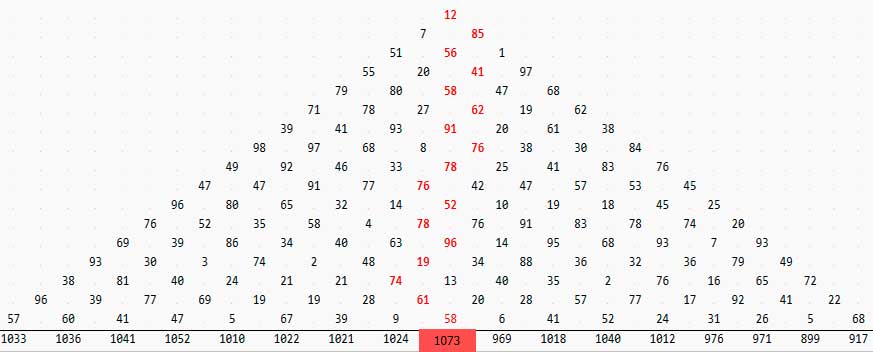
Начнем издалека. Построим треугольник из чисел - случайных чисел. В первой стпроке 1 число, во второй 2, расположенные, так что число верхней строки как бы между ними. В третьей строке - три числа. и т д.

Для построения этого треугольника мы применили программу:
Проблема в том, что надо найти маршрут от вершины до основания треугольника, дающий максимальное значение суммы чисел, встречающихся на нем. От каждого числа можно переходить к следующему числу внизу-слева или внизу справа..
Для 2- х этажного треугольника число возможных маршрутов 21: 10 11: для трех этажного 100. Единица означает "вправо" , а ноль - "влево". При относительно малой высоте треугольника можно посчитать все возможные маршруты и найти лучший ( оптитмальный). А если чиcло этажей велико, очень велико?
Жадный (greedy) алгоритм - алгоритм, заключающийся в принятии оптимальных решений на каждом этапе, допуская, что конечное решение также окажется оптимальным.
Жадный алгоритм обычно предпочитают другим методам оптимизации, таким как динамическое программирование.
Общего критерия оценки применимости жадного алгоритма для решения конкретной задачи не существует,
Однако, для задач, решаемых жадными алгоритмами, характерны две особенности: во-первых, к ним применим
Принцип жадного выбора, а во-вторых, они обладают свойством Оптимальности для подзадач.
Принцип жадного выбора
Говорят, что к оптимизационной задаче применим принцип жадного выбора, если последовательность локально оптимальных выборов даёт глобально оптимальное решение. В типичном случае доказательство оптимальности следует такой схеме:
Доказывается, что жадный выбор на первом шаге не закрывает пути к оптимальному решению: для всякого решения есть другое, согласованное с жадным выбором и не хуже первого.
Показывается, что подзадача, возникающая после жадного выбора на первом шаге, аналогична исходной.
Рассуждение завершается по индукции.
Задача. Монетная система некоторого государства состоит из монет достоинством a1 Жадный алгоритм решения этой задачи таков:
Например, сумму 23 монеты монетами 1, 2, 5 можно предстиавить так: 4 - по 5; 1 по 2 и 1 по 1.
Для данной задачи жадный алгоритм не всегда даёт оптимальное решение, а только для некоторых,
называемых каноническими, монетных систем, вроде используемых в США (1, 5, 10, 25 центов).
Неканонические системы таким свойством не обладают. Так, например, сумму в 24 копейки монетами в 1, 5 и 7 коп.
жадный алгоритм разменивает так: 7 коп. - 3 шт., 1 коп. - 3 шт., в то время как правильное решение - 7 коп. - 2 шт., 5 коп. - 2 шт.[
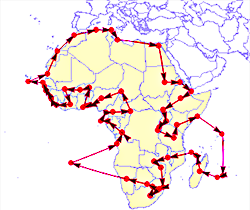
Wolfram Alpha завпрос Shortest tour African capitals/ Например, жадная стратегия для задачи коммивояжера (которая имеет высокую вычислительную сложность )
заключается в следующей эвристике: "На каждом этапе поездки посещайте ближайший не посещаемый город". Эвристика -
Эвристический алгоритм— алгоритм решения задачи, включающий практический метод, не являющийся гарантированно точным.
Эта эвристика не предназначена для поиска лучшего решения, но она заканчивается разумным количеством шагов;
Коммивояжер - бродячий торговец - должен посетить n городов, побывав в каждом городе только раз. Как ему выбрать
кратчайший маршрут. Например, вот, решение в Wolfram Alpha обхода (облета) всех африканскх столиц по оптимальному маршруту.
Вернемся к задаче о максимальном маршруте в треугольнике.
Программа для решения задачи, в которой мы повторяем уже представленный фрагмент кода:
Программа выдает оптимальный (максимальный) маршрут.
И для проверки суммы в каждом ряду треугольника:
Получен наилучший маршрут, но необходимо помнить, что жадный алгоритм может
ошибаться.
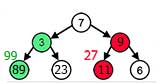
Прирмер неправильной работы жадного алгоритма
.
n = 17;
m = 2 n + 1; kk = n (n + 1)/2;
If[OddQ[n], j0 = Ceiling[m/2], j0 = n + 1];
i = 1; v0 = j0;
mm = ConstantArray[Style[".", 2], {n + 1, m}];
xx = Table[RandomInteger[{1, 99}], {k, 1, kk}];
mm[[1, j0]] = xx[[1]];
k = 1; i = 1; j = j0;
While[k <= kk, If[2 k == i (i + 1), i++;
j0 = j0 - 1; j = j0]; If[i <= n, mm[[i, j]] = xx[[k + 1]]]; k++;
j = j + 2];
Print[Style[Grid[mm, Dividers -> {{}, {n + 1 -> 12}}], 14]]
ss = ConstantArray[0, {n, m}];
j0 = v0;
ss[[1, j0]] = xx[[1]];
ss[[2, j0 - 1]] = xx[[1]] + xx[[2]];
ss[[2, j0 + 1]] = xx[[1]] + xx[[3]];
k = 1;
For[i = 3, i <= n, i++,
For[j = 2, j <= m - 1, j++, a = ss[[i - 1, j - 1]];
b = ss[[i - 1, j + 1]];
If[a > b, mx = a, mx = b];
If[NumberQ[mm[[i, j]]], ss[[i, j]] = mm[[i, j]] + mx]]];
zz = ss;
For[i = 1, i <= n, i++,
For[j = 1, j <= m, j++, If[ss[[i, j]] == 0, ss[[i, j]] = " "]]];
Print[Style[Grid[ss, Dividers -> {{}, {n + 1 -> -1}}], 14]]
xx = Max[zz[[n]]]
px = Position[zz[[n]], xx][[1]][[1]];
ads = {px}; mm[[n, px]] = Style[mm[[n, px]], Red];
For[i = n - 1, i >= 1, i--, j = px;
a = zz[[i, j - 1]];
b = zz[[i, j + 1]];
If[a > b, mx = a, mx = b];
px = Position[zz[[i]], mx][[1]][[1]];
mm[[i, px]] = Style[mm[[i, px]], Red, Bold]];
mm[[n + 1]] = ss[[n]];
Print[Style[Grid[mm, Dividers -> {{}, {n + 1 -> 12}}], 14]]