Числа по спирали
Дано натуральное число n. Необходимо расположить числа от 1 до n2 в квадратном массиве по спирали:
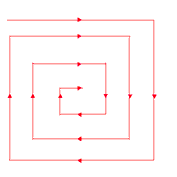
Рисунок. 1
Отсчет начать от левого верхнего угла, далее двигаться в направлении «восток-юг-запад север» и.т.д.
Приведенная ниже программа содержит две процедуры: процедуру вывода массива и процедуру заполнения массива по спирали. В процедуре заполнения массива сначала осуществляется движение от ячейки с индексами [1,1] в направлении «восток-запад» до ячейки [1,n], затем от ячейки [2,n] в направлении «север-юг» до ячейки [n,n], затем в направлении «восток-запад» от ячейки [n,n-1] до ячейки [n,1] и наконец от ячейки [n-1,1] до ячейки [2,1]. Затем все повторяется, но уже с меньшим размером областей.
Program SpiralArray1;
uses crt;
const n = 6;
type
TMx = array[1..n,1..n] of integer;
Procedure Print(mx : TMx);
{Процедура вывода массива}
var
i,j : byte;
begin
writeln; writeln;
for i := 1 to n do begin
writeln;
for j := 1 to n do write(mx[i,j]:2,' ');
end;
end;
Procedure SpiralFill(var mx : TMx);
{Процедура заполнения массива по спирали}
var
i,j,c : byte;
begin
i := 1;
j := 1;
c := 0;
repeat
while (j <= n - c) do
begin
readln(mx[i,j]); inc(j);
end;
{движение в направлении "запад-восток"}
inc(i); dec(j);
while (i <= n - c) do
begin
readln(mx[i,j]); inc(i);
end;
{движение в направлении "север-юг"}
dec(j); dec(i);
while (j >= 1 + c) do
begin
readln(mx[i,j]); dec(j);
end;
{движение в направлении "восток-запад"}
inc( c ); inc(j); dec(i); {параметр с увеличился на 1}
while (i >= 1 + c) do
begin
readln(mx[i,j]); dec(i);
end;
{движение в направлении "юг-север"}
inc(j); inc(i);
until c > n div 2;
end;
var
m : TMx;
begin
clrscr;
SpiralFill(m);
Print(m);
readln;
End.
Рассмотрим другой алгоритм решения этой задачи.
Сначала будем вести отсчет в обратном порядке от n2 до 1, тогда подход к последнему числу матрицы будет осуществляться в направлении «юг - запад - север -восток».
Например для нечетного n, допустим для n=5
| 1 | 2 | 3 | 4 | 5 |
| 16 | 17 | 18 | 19 | 6 |
| 15 | 24 | 25 | 20 | 7 |
| 14 | 23 | 22 | 21 | 8 |
| 13 | 12 | 11 | 10 | 9 |
Последнее число занимает позицию i:=n div 2+1; j:=n div 2+1.
Для четного n, например для n=4, имеем:
| 7 | 8 | 9 | 10 |
| 6 | 15 | 16 | 11 |
| 5 | 14 | 13 | 12 |
| 4 | 3 | 2 | 1 |
При этом последнее число занимает позицию i:=n div 2; j:=n div 2+1.
Перенесем начало координат в позицию последнего числа. Обозначим точку начала координат xx=0; yy=0. Тогда для нечетного n имеем xx:= n div 2+1-j; yy:= n div 2+1-i, для четного n xx:= n div 2+1-j; yy:= n div 2-i. При этом положительное направление оси абсцисс выберем в направлении «с востока на запад».
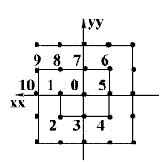
Риснок. 2
Таким образом, если n=5, то для x[2,1]=16 имеем xx=2+1-1=2, yy=2+1-2=1. Для n=4, x[2,1]:=6, имеем xx:=2+1-1=2, yy=2-2=0. Далее рассмотрим спиральную функцию двух переменных S=F(xx ,yy), которая ставит в соответствие упорядоченной паре целых чисел xx,yy некое натуральное число S [1]. Схематически спиральная функция представлена на рис 2.
Например, для упорядоченной пары xx=-1; yy=1 S=F(-1,1)=6. Функция S=F(xx,yy) может быть представлена по формуле:
| S=(2k)2+p[2k+xx+yy], | |||
| где | k=Max(|xx|,|yy|)- максимальное значение из двух; | ||
| p=1, если xx>yy, иначе p=-1. | |||
Очевидно, чтобы в массиве располагались числа от n2 до 1 необходимо ввести поправку, т.е S:=n2-S. И наконец для четного n матрицу необходимо повернуть на 180° против часовой стрелки, чтобы отсчет соответствовал условию задачи, т.е. был в направлении «восток-юг-запад-север».
Program SpiralArray1;
uses crt;
const n = 6;
type
TMx = array[1..n,1..n] of integer;
Procedure Print(mx : TMx);
{Процедура вывода массива}
var
i,j : byte;
begin
writeln; writeln;
for i := 1 to n do begin
writeln;
for j := 1 to n do write(mx[i,j]:2,' ');
end;
end;
Procedure SpiralFill(var mx : TMx);
{Процедура заполнения массива по спирали}
var
i,j,c : byte;
begin
i := 1;
j := 1;
c := 0;
repeat
while (j <= n - c) do
begin
readln(mx[i,j]); inc(j);
end;
{движение в направлении "запад-восток"}
inc(i); dec(j);
while (i <= n - c) do
begin
readln(mx[i,j]); inc(i);
end;
{движение в направлении "север-юг"}
dec(j); dec(i);
while (j >= 1 + c) do
begin
readln(mx[i,j]); dec(j);
end;
{движение в направлении "восток-запад"}
inc( c ); inc(j); dec(i); {параметр с увеличился на 1}
while (i >= 1 + c) do
begin
readln(mx[i,j]); dec(i);
end;
{движение в направлении "юг-север"}
inc(j); inc(i);
until c > n div 2;
end;
var
m : TMx;
begin
clrscr;
SpiralFill(m);
Print(m);
readln;
End.
1. Грэхем Р., Кнут Д., Паташник О. Конкретная математика. Основание информатики.
-М.: Мир, 1998. -703 с.
Назад

