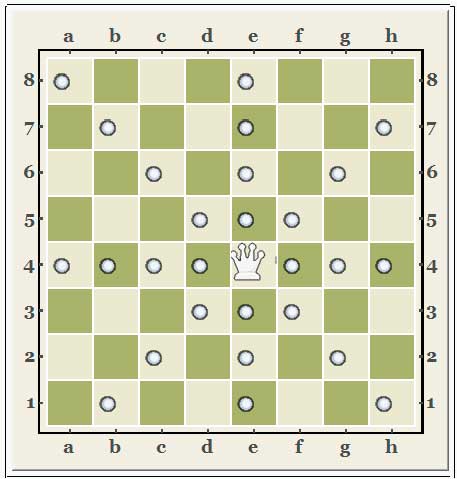
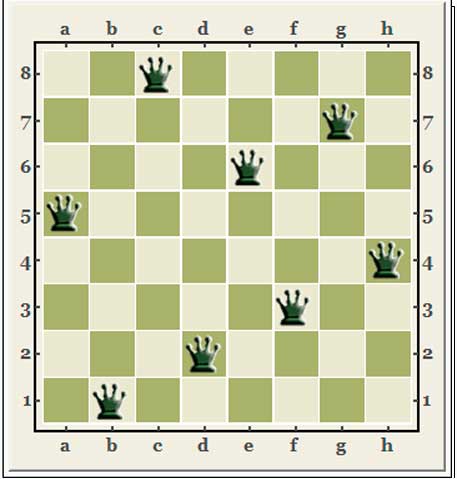
Несколько, на наш взгляд интересных задач, связанных с шахматами. Среди них есть известные задачи, например: о числе способов расставмть на доске 8х8 8 не атакующих друг друга ("мирных") ферзей, так и менее известные:

Эти задачи можно отнести к важному и интересному разделу математики "комбинаторика", но с другой стороны, решение этих задач на практике требует безусловного применения компьютера и программного обеспечения. Возникает проблема, к какому разделу отнести эти задачи: "Математика" или "Информатика". Решили, и не к тому и не к другому. Математика дает направление решения, предоставляет алгоритм решения, а информатика предоставляет инструментарий для получения конкретного ответа.

В 1998 году в издательстве "Мир" вышла книга "Конкретная математика. Основание информатики" - Дональда Кнута, Роналда Грэхема и Орена Паташника по математике, рассматривающая математические основы информатики, особенно анализа алгоритмов. Вынесенный в заглавие книги термин конкретная математика произошёл от слияния двух других - КОНтинуальная и дисКРЕТНАЯ. Так подчёркивается, что в книге читателю представляется техника оперирования с дискретными объектами, сходная с традиционными методами математического анализа. Кроме того, конкретная математика противопоставляется традиционной абстрактной, авторы замечают:

Погоня за обобщениями оказалась столь захватывающей, что целое поколение математиков потеряло способность находить прелесть в частностях, в том числе получать удовольствие от решения численных задач или оценить по достоинству роль математических методов. Абстрактная математика стала вырождаться и терять связь с действительностью - математическое образование нуждалось в конкретном противовесе для восстановления устойчивого равновесия ..

Континуальная - значит непрерывная. Слова-антонимы - "дискретная" и "концептуальная" вместе образуют название нового направления в математике, которое связано с компьютерами, алгоритмами - с информатикой- конкретную математику.

Мощным инструментом решения задач конкретной математики явдяется пакет программ Wolfram Mathematica

Сначала создадим файл - картинку с фигурами, соблюдая строго размеры. У нас каждая фигура в квадрате 45х45 px, 7 фигур x45=315px, два цвета 2х45=90 px. Картинка 315х90, обязательно на прозрачном фоне - файл png.

Программа начальной расстановки фигур

...............

Расстановка фигур на доске - в выделеном фрагменте. Оставив aa={};, получим пустую доску.

Поставим одного белого ферзя на поле e4. В принятой нами записи e4 запишется как {5,4}, ферзь закодирован цифрой 4. Тогда aa={chessFigureShow[4,White,{5,4}]};

Пометим (7-метка) поля, которые атакует наш ферзь. Во-первых, он бьет поля по вертикали и по горизонтали где он стоит.

Восемь мирных ферзей

Решение

• Во - первых, каждый из 8 ферзей должен занимать СВОЮ вертикаль, на каждой из 8 вертикалей должен быть ферзь.
• Пометим вертикали доски не a,b,c...h, а 1,2,3....8, горизонтали оставим как есть 1,2,3....8.. Тогда положение 8 ферзей на доске можно записать 8 значным числом без повтторяющихся цифр и без цифр 0 и 9. Например, 51826374, представляет такую расстановку. ,
  

  Эта расстановка не подходит, так как две пары ферзей атакуют друг друга. Это ферзи 3-5 и 1-4 - их позиции (цифры в числе 51826374)

• Условие «одной диагонали » n+m==i+j или n-m==i-j. Для каждого числа расстановки ферзей введем два числа: сумма цифры и ее позиции, разность цифры и ее позиции.
• Для числа 51826374 это будут числа 6 3 11 6 11 9 14 12 и 4 -1 5 -2 1 -3 0 -4. В первой последовательности числа 6 и 11 встречаются по два раза.
• Конечно можно просмотреть в цикле все восьмизначные числа от 12345678 до 87654321 и выбирать нужные, при этом надо просмотрреть 87654321--12345678=75308643 чисел, но можно генерировать перестановки 8 цифр , этих перестановок будет 8!=40320 и в них выбирать подходящие.

Итак, 92 способа расставить 8 ферзей на доске 8х8, так чтобы никакие два из них не атаковали друг друга. Pаспечатаем хотя бы несколько из них.

Результат работы программы

>> >