Чтобы дать минимальные сведения о рисовании кривых на экране, рассмотрим, в качестве примера, как на экране получить обыкновенную окружность. Вспомним три способа задания окружности. Первый и наиболее привычный способ знаком со школы:

Это уравнение множества точек, лежащих на окружности. Любая точка с декартовыми (прямоугольными) координатами лежит на окружности тогда и только тогда, когда сумма квадратов x и y равна квадрату радиуса окружности r.

Приведенной формулой можно воспользоваться для составления программы, рисующей окружность, если разделить кривую на две части - верхнюю и нижнюю. Переменная x пробегает через последовательные значения от -r до r. Переменная y вычисляется для каждой ветви кривой (верхней и нижней):

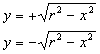На Турбо Паскале это выглядит так:

Program Test_1; 
Uses CRT, Graph; 
Var d,m,r,y:integer; 
x:real; 
Begin 
{установка графического режима} 
d:=detect; m:=detect; 
InitGraph(d,m,''); 
{----------------------------} 
r:=100; {радиус окружности} 
x:=-r; 
while x<=r do begin 
y:=round(sqrt(r*r-x*x)); 
{окружность с центром в точке 320, 240} 
PutPixel(320+round(x),240+y,white); 
PutPixel(320+round(x),240-y,white); 
x:=x+0.01; 
end; 
{ждать нажатия клавиши} 
repeat 
until KeyPressed; 
CloseGraph {закрыть графический режим} 
End. 

Такое задание кривой выглядит несколько неуклюже. Попробуем перейти к полярным координатам.

В декартовой системе координаты точки x, y указывают удаление точки по горизонтали и вертикали от некой центральной точки, называемой началом отсчета (в нашей программе это точка с координатами 320, 240).

Полярные координаты R, θ  определяют точку совсем по - другому: R-расстояние от точки до начала отсчета, θ  — угол между линией, соединяющей данную точку с точкой начала отсчета, и горизонтальной прямой. Уравнение окружности в полярных координатах имеет очень простой вид R=r.

Независимо от величины угла  θ  расстояние R всегда равно радиусу окружности r. К сожалению, программа для изображения окружности в полярных координатах весьма сложна и мы её не приводим.

Третье представление основано на так называемых параметрических уравнениях. Для окружности они имеют вид:

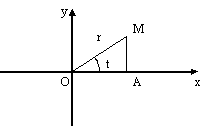
Эти уравнения очевидны из рисунка.

	OM=r; OA=x=r cos(t) ; AM=y=r sin(t)

Если параметр t заставить принимать значения от 0 до 2π, то точка M будет описывать окружность. Часть программы будет выглядеть так:

t:=0; r:=100; 
while t<=2*pi do 
begin 
x:=round(320+r*cos(t)); 
y:=round(240+r*sin(t)); 
{окружность с центром в 
точке 320, 240} 
PutPixel(x,y,white); 
t:=t+0.01 
end; 

С помощью параметрических уравнений можно задать весьма занимательные фигуры. Например, эллипс задается следующими уравнениями:

Если взять  r1>r2,  то эллипс будет вытянут вдоль оси x и наоборот —  при r1<r2 он вытянется вдоль оси y.

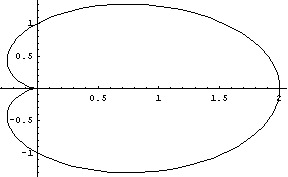
Уравнения кардиоиды - кривой напоминающей человеческое сердце:

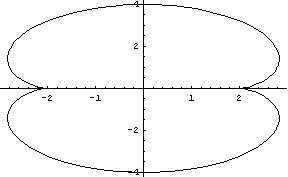
Параметрические уравнения нефроиды - кривой представлющей почки:

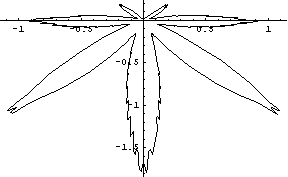
В Сети существует множество сайтов, посвященных параметрическим кривым [1-3]. Названия этихк кривых звучат весьма загадочно: ведьмин локон, астроида, циклоида, лемнисиката Бернулли, декартов лист и т.п. Получено уравнение кривой под названием каннабола - напоминающей лист конопли [4,5]:

R = (1 - Sin(t))·(1 - .9·|(Sin[4t)|)·(.9 - .05·Cos(200t)) x = R·Cos(t) y = R·Sin(t)

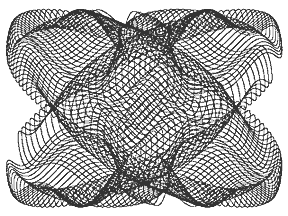
Вот еще одна кривая, которая носит название «безумие» (madness)[6]

x = Sin(0.0099t)-0.7Cos(0.0301t) y = 0.1Sin(0.1503t)+Cos(0.0101t)

Программа для рисования этой кривой:

Program Madness; 
Uses CRT, Graph; 
Var d,m,x,y :integer; 
t:real; 
Begin 
d:=detect; 
m:=detect; 
InitGraph(d,m,''); 
t:=0; 
repeat 
x:=320+round(180*(sin(0.0099*t)-0.7*cos(0.0301*t))); 
y:=240-round(200*(0.1*sin(0.1503*t)+cos(0.0101*t))); 
PutPixel(x,y,white); 
t:=t+0.01; 
until KeyPressed; 
CloseGraph; 
End.

Естественно, при рисовании, например кардиоиды, надо параметр t менять от 0 до 2π, используя цикл while, а её центр поместить в центр экрана (320, 240).

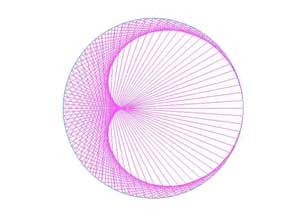
	Кардиоида.

Кстати, кардиоиду можно изобразить не прибегая к параметрическим кривым. Возьмем окружность, разобьем её на 144 равные дуги. При обходе окружности пронумеруем точки дважды: сначала от 1 до 144, затем от 145 до 288. Точку 1 соединим линией (хордой) с точкой 2, точку 2 соединим с точкой 4, точку 3 с точкой 6 и т.д., точку 144 соединим с точкой 288. Пересечения хорд образуют кардиоиду.

Программа для рисования кардиоиды:

Сохранить эту программу

Продолжим рассмотрение задач компьютерной графики [7].

На первый взгляд приведенный рисунок кажется достаточно сложным, но при более пристальном рассмотрении оказывается, что он представляет собой последовательность вложенных друг в друга квадратов. Эти квадраты не только становятся все меньше и меньше, но поворачиваются на постоянный угол.

Допустим исходный квадрат имеет вершины с координатами (x[i], y[i]), где i=1,2,3,4, a i-ая сторона квадрата является линией, соединяющей вершину с координатами (x[i], y[i]) с вершиной (x[i+1], y[i+1]), при этом, дополнительно предположим, что если i=4, то i+1 будет равным 1, т.е. 4+1=1 (это называется сложением по модулю 4). Каждая сторона квадрата рассекается точкой (x'[i],y'[i]) в отношении  μ/(1-μ),  где 0≤ μ ≤1. Параметр  μ  равен отношению расстояний от (x[i], y[i]) до (x'[i],y'[i]) и от (x'[i],y'[i]) до (x[i+1], y[i+1]).

Следовательно (x'[i],y'[i]) = (x[i](1- μ)+x[i+1]μ, y[i](1- μ)+y[i+1]μ)

Program Cardioid; 
Uses CRT, Graph; 
Const n=144; 
r=200; 
t=2*pi/n; 
Var x,y: array[1..2*n] of integer; 
i,d,m:integer; 
Begin 
d:=detect; m:=detect; 
InitGraph(d,m,''); 
SetColor(LightRed); 
Circle(340,240,r); 
for i:=1 to n do begin 
x[i]:=340+round(r*cos(i*t)); 
y[i]:=240+round(r*sin(i*t)); 
x[i+n]:=x[i]; 
y[i+n]:=y[i] 
end; 
SetColor(green); 
for i:=1 to n do line(x[i],y[i],x[i*2],y[i*2]); 
repeat 
until KeyPressed; 
CloseGraph 
End. 

Полученные в результате поворота квадратов кривые называют кривыми преследования. По траектории, совпадающей с кривой преследования, перемещается, например, собака, находящаяся сначала в вершине исходного квадрата и бегущая прямо на зайца, который бежит к центру квадрата из другой вершины. По кривой преследования перемещается самонаводящаяся ракета, летящая к движущейся цели.

Мы выяснили, как можно изобразить эллипс и как повернуть квадраты. Рассмотрим, как можно получить эллипс, повернутый на заданный угол  α . Для этого к каждой точке эллипса с координатами (x,y) надо применить преобразование поворота.

Для того чтобы получить эти уравнения нужно взять точку в прямоугольной системе координат (x',y') , а затем повернуть систему координат на угол  α, в новой системе координат точка будет иметь координаты (x,y).

Необходимо получить зависимость координаты x' от x и y' от y. Угол  α  закрашен красным цветом. Тогда OA=OCcosα=xcosα  PC=MCsinα=ysinα  OB=x'=xcosα-ysinα  MP=MCcosα=ycosα  PB=CA=OCsinα=xsinα  BM=y'=xsinα+ycosα

Program Ellipses; 
Uses CRT, Graph; 
Var d,m,x,y:integer; 
xx,yy,t,a:real; 
Const 
{Центр экрана} 
xo=320; yo=240; 
Begin 
d:=detect; m:=detect; 
InitGraph(d,m,''); 
a:=0; 
{Изменение угла поворота} 
while a<=2*pi do begin 
t:=0; 
while t<=2*pi do begin 
{Координаты эллипса} 
xx:=200*cos(t); 
yy:=80*sin(t); 
{Поворот} 
x:=round(xo+(xx*cos(a)-yy*sin(a))); 
y:=round(yo-(xx*sin(a)+yy*cos(a))); 
PutPixel(x,y,white); 
t:=t+0.001; 
end; 
a:=a+pi/20; 
end; 
repeat 
until KeyPressed; 
CloseGraph 
End. 

Приведенная программа рисует 20 поворачивающихся эллипсов.

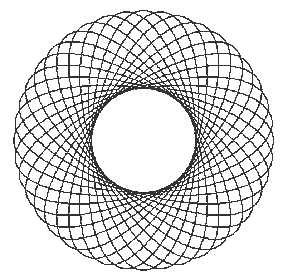
Наконец программа, рисующая вращающийся кубик.

Program Cubik';
Uses CRT, Graph; 
Type a_t=array [1..8] of integer; 
Procedure Cubik(x,y:a_t;c:integer); 
{Процедура рисования кубика, 
координаты вершин в массивах х,y} 
Begin 
SetColor(c); 
line(x[1],y[1],x[2],y[2]); 
line(x[2],y[2],x[3],y[3]); 
line(x[3],y[3],x[4],y[4]); 
line(x[4],y[4],x[1],y[1]); 
line(x[5],y[5],x[6],y[6]); 
line(x[6],y[6],x[7],y[7]); 
line(x[7],y[7],x[8],y[8]); 
line(x[8],y[8],x[5],y[5]); 
line(x[1],y[1],x[5],y[5]); 
line(x[2],y[2],x[6],y[6]); 
line(x[3],y[3],x[7],y[7]); 
line(x[4],y[4],x[8],y[8]); 
End;

1. Википедия. Кривые
2. Параметрические кривые
3. Графики основных функций
4. Каннабола. Российскими учеными выведена формула конопли
5. Каннабола. Арбузный форум
6. Madness curve
7. Эйджел Й. Практическое введение в машинную графику. М.: Радио и связь, 1984. - 136 с.

Назад