Back To Up
%>
 
     
Э.М. Зарипова

Задачи. Красивые решения

В школьном курсе информатики, говоря о свойствах алгоритма, обычно упоминают следующие.

Дискретность (прерывность, раздельность) — алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.

Определенность — каждое правило алгоритма должно быть четким, однозначным. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.

Результативность (конечность) — алгоритм должен приводить к решению задачи за конечное число шагов.

Массовость — алгоритм решения задачи разрабатывается в общем виде, то есть он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.

Однако. есть и другие свойства вычислительных алгоритмов, которые часто не упоминаются, например выполнимость, т.е получение результата вообще, а не за приемлемое число шагов. Пример не выполнимого алгоритма: «Вычислить максимальное число меньше 1». Красота алгоритма определяется его необычностью, неординарностью и краткостью. Например, поменять содержимое ячеек памяти А и B можно так: С:=A; A:=B; B:=C. Вводится дополнителная память С. В случае числовых типов данных можно поступить так: A:=A+B; B:=A-B; A:=A-B. Красиво, хотя красота — категория субъективная.

Еще пример. Числа в десятичной записи состоящие исключительно из единиц называют «репьюниты». Необходимо получить репьюнит 30 порядка (30 единиц) и проверить, является ли он простым числом.

Здесь, как и в остальных случаях прменяем Wolfram Mathematica 11. 

a=(10^30-1)/9;
PrimeQ[a]
                  False
FactorInteger[a]

CenterDot @@ (Superscript @@@ %)
          {{3, 1}, {7, 1}, {11, 1}, {13, 1}, {31, 1}, {37, 1}, {41, 1}, {211, 
            1}, {241, 1}, {271, 1}, {2161, 1}, {9091, 1}, {2906161, 1}


  31·71·111·131·311·371·411·2111·2411·2711·21611·90911·29061611

Известно только 9 простых репьюнитов [3]: R(n); n={ 2, 19, 23, 317, 1031, 49 081, 86 453, 109 297, 270 343}

При этом, по состоянию на август 2014, простота последних четырех чисел в вышеуказанной последовательности не доказана, а лишь предполагается с некоторой вероятностью[3]. Очевидно, что индексы простых репьюнитов также являются простыми числами.

Перейдем к другим задачам.

[]- Последовательность A004023 в OEIS

1.    Рассмотрим простые числа, десятичная запись которых заканчивается на 999999. Первым таким числом, в порядке возрастания, является число 2999999. 999-ым числом является 8878999999. Чему равно 999999-ое простое число, заканчивающееся на 999999? 

tm = SessionTime[];
k = 0; i = 1;
While[k < 999999, If[PrimeQ[i*1000000 - 1], k++]; i++];
(i - 1) 10^6 - 1
Print["Время счета, с=  : ";SessionTime[] - tm

Берем натуральное i, умножаем его на 1000000 и из произведения вычитаем 1, получаем число заканчивающиеся на 999999, которое проверяем на простоту.

11623831999999
Время счета, с= : 362.5377360
https://seanhamptoncole.wordpress.com/2013/03/26/living-strategically-50-lessons-chess-teaches-you-about-life/?wref=tp


2.   Разместите простые числа в ряд по возрастанию: 2, 3, 5, 7, 11, 13,... Суперпростые числа - это числа в ряду простых чисел, порядковый номер которых также является простым числом. Сколько всего суперпростых чисел меньших 107? 

PrimePi[PrimePi[10^7]]
  1. Находим простые числа меньшие 107.
  2. Считаем количество найденных простых чисел. Получаем число N.
  3. Находим простые числа до N включительно.
  4. Считаем их количество.
Ответ: 53911


3.   КОТ + ПЁС = 1000. Найдите максимум суммы К+О+Т+П+Ё+С.

Глядя на условие, можно его представить иначе: разбить1000 на два слагаемых,каждое из которых содержит три различные цифры и не начинается с 0.

Разобъем 1000 на два слагаемых 

IntegerPartitions[1000,{2}]

из полученных вариантов {{999, 1}, {998, 2}, {997, 3},...{875, 125}, {874, 126}, {873, 127}, {872, 128}, {871, 129}, ....{500,500}} нам подходят только те, что содержат три цифры, т.е. в которых количество цифр в каждой части равно друг другу:...{875, 125}, {874, 126}, ... 

Select[IntegerPartitions[1000,{2}],Length[IntegerDigits[
First[#]]]==Length[IntegerDigits[Last[#]]]&]

но это должны быть разные цифры, например {875, 125} не годится , а {874, 126} подходит, т.е. должно быть 6 различных цифр: 

Select[IntegerPartitions[1000, {2}], Length[IntegerDigits[First[#]]] ==
  Length[IntegerDigits[Last[#]]] && Length[Union[IntegerDigits[First[#]] ,
    IntegerDigits[Last[#]]]] ==6 &]

В итоге получаем подходящие разбиения: {{897, 103}, {896, 104}, {894, 106}, {893, 107}, {876, 124}, {874, 126}, {857, 143}, {853, 147}, {847, 153}, {843, 157}, {826, 174}, {824, 176}, {807, 193}, {806, 194}, {804, 196}, {803, 197}, {796, 204}, {794, 206}, {786, 214}, {784, 216}, {769, 231}, {761, 239}, {759, 241}, {751, 249}, {749, 251}, {741, 259}, {739, 261}, {731, 269}, {716, 284}, {714, 286}, {706, 294}, {704, 296}, {698, 302}, {692, 308}, {679, 321}, {671, 329}, {659, 341}, {658, 342}, {652, 348}, {651, 349}, {649, 351}, {648, 352}, {642, 358}, {641, 359}, {629, 371}, {621, 379}, {608, 392}, {602, 398}, {598, 402}, {597, 403}, {593, 407}, {592, 408}, {587, 413}, {583, 417}, {579, 421}, {571, 429}, {569, 431}, {568, 432}, {562, 438}, {561, 439}, {539, 461}, {538, 462}, {532, 468}, {531, 469}, {529, 471}, {521, 479}, {517, 483}, {513, 487}, {508, 492}, {507, 493}, {503, 497}, {502, 498}}, в которых выделяем цифры и находим суммы цифр. 

Total /@ Flatten /@ IntegerDigits /@Select[IntegerPartitions[1000,{2}],
Length[IntegerDigits[First[#]]]==Length[IntegerDigits[Last[#]]]&&
 Length[Union[ IntegerDigits[First[#]] , IntegerDigits[Last[#]]]] ==6 &]

Все суммы равны 28. Ответ: 28.

Пока писал это решение догадался до еще более простого: 

   aa = Select[Table[a, {a, 102, 498}], 
   Length[Union[IntegerDigits[#], IntegerDigits[1000 - #]]] == 6 &];
Partition[Riffle[aa, 1000 - aa], 2]

Решение в подобных головоломок общем виде

Криптарифм можно считать хорошим, если в результате шифрования получилась какая-то осмысленная фраза. Например, классическим криптарифмом является пример на сложение, придуманный Генри Э. Дьюдени (Henry Ernest Dudeney).

В 1924 году в июньском номере журнала "Strand Magazine" (в конце XIX века сэр Артур Конан Дойль писал Шерлока Холмса специально для этого издания) Дьюдени публикует ребус:

SEND + MORE = MONEY.

Генри Эрнест Дьюдени ( 1857 -1950.)        Подробнее 
X

Квадратура равностороннего треугольника

Родился на юге Англии, в графстве Суссекс. Его дед был простым пастухом и большим любителем математики, которую он изучал самостоятельно, а впоследствии даже преподавал, став школьным учителем в небольшом городке Льюис, неподалеку от Лондона. Учителем был и отец Генри. Самому Дьюдени также не довелось изучать математику в колледже. Как и его дед, он был талантливым самоучкой

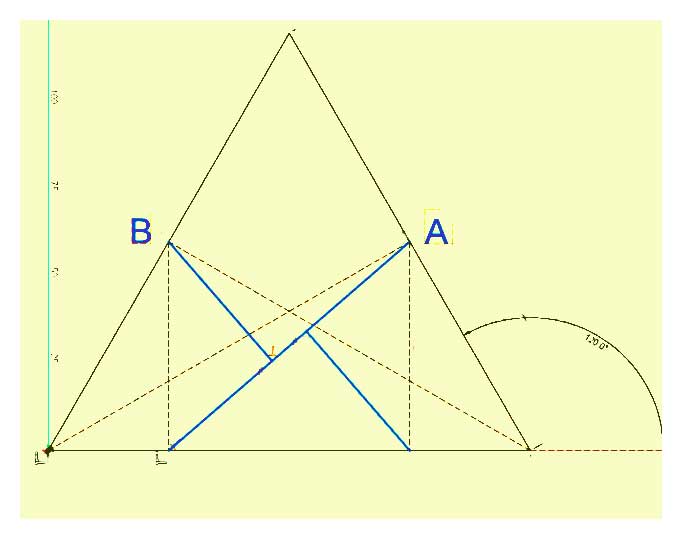
На какое минимальное число частей необходимо разбить равносторонний треугольник, чтобы из них можно было сложить квадрат? Эта задача была предложена читателям газеты «Дейли мейл» Генри Дьюдени в выпусках от 1 и 8 февраля 1905 года. Среди сотен полученных ответов правильным был всего один: достаточно четырёх частей.

Как же догадаться до такого разбиения? Необходимо взять равновеликие треугольник и квадрат, а затем составить из каждой фигуры регулярную полоску. Наложив одну полоску на другую так, чтобы максимальное число середин сторон одной полосы попадало на стороны другой полосы, получаем искомое разбиение. Это, в каком-то смысле, общий способ нахождения разбиений равновеликих многоугольников.

Читать полностью: http://www.etudes.ru/ru/models/dudeney-dissection/ © 2002—2019, Математические этюды

В переводе с английского языка эта фраза означает «шлите больше денег» - лаконичный текст телеграммы, предположительно, посланной студентом колледжа к родителям. Кроме того, имеется еще одно требование к правильному криптарифму: он должен иметь единственную возможную расшифровку. Например, единственным (правильнным) решением криптарифма Дьюдени является 9567+1085=10652.



U S A У Д А Р S E N D
+ U S S R или + У Д А Р или + M O R E
P E A C E Д Р А К А M O N E Y

Часть задачи решает Человек, часть задачи решает Машина — некий симбиоз. В первой задаче Догадаемся, что U=9, а P=1; E=0. Пока мозг не подключен к Машине, обратимся к ней. 

     For[s = 2, s <= 8, s++, 
      If[ s != a && s != r && s != c && 
        900 + 10 s + a + 9000 + 
		100 s + 10 s + r == 
         10000 + 100 a + 10 c, 
 Print[9, s, a, "+", 9, s, s, r, " 
 =", 1, 0, a, c, 0]]]]]]];
 
	   
	932+9338 =10270


Во второй задаче заменим кириллицу латиницей: U,D,A,R,K. D=1; U≠0. Мало того U=5,6,7,8,9. A=0,2,4,6,8 

For[u = 5, u <= 9, u++,
 For[a = 0, a <= 8, a += 2,
  If[u != a,
   For[r = 0, r <= 9, r++, 
    If[r != a && r != 1 && r != u, 
     For[k = 0, k <= 9, k++, 
      If[
       k != 1 && k != a && k != u && 
        k != r && (1000 u + 100 + 10 a + r) 2 == 
         10000 + 1000 r + 100 a + 10 k + a, 
       Print[u, 1, a, r, "+", u, 1, a, r, "=", 1, r, a, k, a]]]]]]]]

	   
	   
	   8126+8126=16252

Третья задача-задача Г. Дьюдени : M=1; 0=0. 

For[s = 2, s <= 9, s++,
  For[e = 2, e <= 9, e++,
   For[n = 2, n <= 9, n++,
    For[d = 2, d <= 9, d++,
      For[r = 2, r <= 9, r++,
       For[y = 2, y <= 9, y++,
        aa = {s, e, n, d, r, y};
        If[DeleteDuplicates[aa] == aa, 
         If[1000 s + 100 e + 10 n + d + 1000  + 10 r  + e == 
           10000 + 100 n + 10 e + y, 
		  Print[" ", s, e, n, d];
          Print[" ", 1, 0, r, e];
          Print["______________"];
          Print[  1,0, n, e, y]]]]]]]]]];
		  
		 9567
		+1085
		_____
		10652

Немного усложним задачу, никаких букв одни звездочки, вместо котоых надо поставить цифры. Все же кое какая информация есть, используем ее, оставив тот же принцип перебора

* * *
x * 2 *
* * *
+ * * * *
* 8 *
* * 9 * 2 * 




For[a = 100, a <= 999, a++,
 For[b = 100, b <= 999 b++,
  bb = IntegerDigits[b];
  If[bb[[2]] == 2 && IntegerLength[bb[[3]] a] == 3  &&
    IntegerLength[2 a] == 4, z = bb[[1]] a; zz = IntegerDigits[z];
   If[zz[[2]] == 8 && IntegerLength[z] == 3,
    y = a b; yy = IntegerDigits[y];
    If[Length[yy] == 6 && yy[[3]] == 9 && yy[[5]] == 2, 
     Print[{a, b, y}]]]]]]
	 
	 {987,121,119427}
9 8 7
x 1 2 1
9 8 7
+ 1 9 7 4
9 8 7
1 1 9 4 2 7

Стефан Барр предложил следующий криптарифм:

ROME-SUM=RUSE

Все попытки решить который приводят к неудаче. Здесь «изюминка» в уменьшаемом ROME - РИМ, ведь кроме арабских цифр имеются и римские. Английская пословица наставляет:

When in Rome,do as Romans do -

  • В Риме поступай как римлянин;
  • В чужой монастырь со своим уставом не лезут;
  • В Тулу со своим самоваром не ходят;
  • С волками жить, по волчи выть и т.п.

Древние римляне различали 8 цифр:

  • I - Unus, una, unum (один)
  • V - Quinque (пять)
  • X - Decem (десять)
  • L - Quinquaginta (пятьдесят)
  • C - Centum (сто)
  • D - Quingenti (пятьсот)
  • M - Mille (тысяча)
  • M- Decies centies milia (десять сотен тысяч = миллион)

Кстати, слово миллион было придумано путешественником Марко Поло уже после того, как все древние римляне растворились в других народах. 

x1 = {}; x2 = {}; xc2 = {}; xc1 = {};
For[a = 1, a <= 5000, a++,
  rr = RomanNumeral[a];
  ll = StringLength[rr];
  cc = Characters[rr];
  If[ll == 4 && cc == DeleteDuplicates[cc], x1 = AppendTo[x1, rr]; 
   xc1 = AppendTo[xc1, cc]];
  If[ll == 3 && cc == DeleteDuplicates[cc], 
   x2 = AppendTo[x2, {"_" <> rr}]; 
   xc2 = AppendTo[xc2, Flatten[{" ", cc}]]]];
l4 = Length[xc1];
l3 = Length[xc2];

xc1
(*ROME-SUM=RUSE*)
xc2
k = 0;
For[i = 1, i <= l4, i++,
 t1 = xc1[[i]];
 For[j = 1, j <= l3, j++,
  t2 = xc2[[j]];
  If[t1[[3]] == t2[[4]] && t1[[1]] != t2[[2]] && t1[[1]] != t2[[3]], 
   nt1 = FromRomanNumeral[StringJoin[t1]];
   
   
   nt2 = FromRomanNumeral[StringJoin[Rest[t2]]];
   If[nt1 - nt2 > 0 && 
     MemberQ[xc1, Characters[ RomanNumeral[nt1 - nt2]]],
    ccz3 = Characters[ RomanNumeral[nt1 - nt2]];
    
    If[ccz3[[1]] == t1[[1]] && ccz3[[2]] == t2[[3]] && 
      ccz3[[3]] == t2[[2]],
     
     k++;
     Print[k, " ", nt1, "  ", nt2, "  ", nt1 - nt2, "  ", t1, "  ";
DCVI-LXV=DXLI
or in Arabic numeral's: 606-65=541.
  1. 606 45 561 {D,C,V,I} { ,X,L,V} {D,L,X,I}
  2. 606 65 541 {D,C,V,I} { ,L,X,V} {D,X,L,I}
  3. 1106 45 1061 {M,C,V,I} { ,X,L,V} {M,L,X,I}
  4. 1106 65 1041 {M,C,V,I} { ,L,X,V} {M,X,L,I}
Nice,is it not? That was my original answer.



  


  1. http://novijmir.blogspot.ru/p/blog-page_21.html
  2. http://www.stihi.ru/2010/03/15/2794
  3. https://www.math.uni-bielefeld.de/~sillke/PUZZLES/ALPHAMETIC/
  4. http://school.komi.com/puz_olymp/puzzles/PuzzlesRRP/Com/Content.htm
  5. Барр С. Россыпи головоломок







  • Задачи. Красивые решения
  • Перельман Я.И. I
  • Перельман Я.И. II
  • :Жаднный алгоритм