ОСНОВЫ
МАТЕМАТИЧЕСКОЙ
ЛОГИКИ

Аксиомы и теоремы алгебры логики

Аксиома постулат — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое при доказательстве других её положений, которые, в свою очередь, называются теоремами[1].

Под логической аксиомой понимается формула логико-математического языка, принимаемая в качестве аксиомы при построении формальной теории, истинная в любой структуре для данного языка в силу смысла логических символов. Логические аксиомы выбираются таким образом, чтобы множество логических следствий из аксиом в точности совпадало с множеством теорем.

Алгебра логики строится на основе следующих аксиом:

1. Переменная может принимать лишь одно из двух возможных значений:

   x=0, если x ≠1 ;x=1, если x≠0 .

2. Вводится преобразование, называемое инверсией, такое, что

   

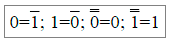
3. Вводится преобразование, называемое дизъюнкцией, для которого справедливы соотношения:

   x∨x=x; x∨1=1; x∨0=x; x∨x=1 .

4. Вводится преобразование, называемое конъюнкцией, для которого справедливы соотношения:

   x∧x=x; x∧1=x; x∧0=0; x∧x=0

Соотношения 1-4 проверяются подстановкой логических значений «0» и «1».

На основе рассмотренных выше аксиом, выводятся теоремы, содержащие основные законы алгебры логики:

1. Коммутативный (переместительный) закон:

   x∨y=y∨x; x∧y=y∧x

2. Ассоциативный (сочетательный) закон:

   x∨(y∨z)=(x∨y)∨z=x∨y∨z; (x∧y)∧z=x∧(y∧z)=x∧y∧z
   
   
   
   

3. Дистрибутивный (распределительный) закон:

   x∧(y∨z)=x∧y∨x∧z; x∨y∧z=(x∨y)∧(x∨z)

4. Законы поглощения:

   x ∧(x∨y)=x; x∨x∧y=x

5. Закон склеивания:

   x ∧y∨x∧y=x ;

6. Законы инверсии (теоремы де Моргана):

   x∨y∨z=x∧y∧z; x∧y∧z=x∨y∨z

7. Законы Порецкого

   x∨x∧y=x∨y; x∧(x∨y)=x∧y

8. Представление импликации

   x → y=x∨y

   Платон Сергеевич Порецкий 1846-1907	Oгастес де Морган 1806-1871

   Справедливость любого закона можно доказать разными методами. Проще всего это можно сделать прямой подстановки вместо переменной значений 0 и 1. Ряд законов доказывается методом перебора всех возможных значений переменных, для которых проверяется справедливость закона. Для доказательства закона достаточно показать тождественность выражений, образующих левую и правую стороны доказываемого соотношения при всех наборах переменных, принимающих значения 0 или 1, что делается с помощью таблиц истинности.

   Приоритет выполнения логических операций:

   1. операции в скобках;
   2. инверсия, NOT;
   3. конъюнкция, AND; штрих Шеффера NAND
   4. дизъюнкция OR, стрелка Пирса NOR
   5. исключающее ИЛИ XOR, эквивалентность EQV;
   6. импликация IMP
   
   

   Несколько примеров на упрощение логических выражений:

   1. (x∧y ∨z) ∧(x∨y)∨z= x∧z∨y∧z∨z=x∨y∨z — здесь применены дистрибутивный закон и закон Порецкого.
      
      
      
   2. (x∧y∨ ¬z)=(x∨y)∧z — здесь применены правила де Моргана и двойного отрицания.
       
      
      
   3. x∧y∨x∨y∨x=x∧y∨x∧y∨x=1 — здесь применены правило де Моргана, правила 3 для дизъюнкции.
   4. a∧b∨(a∧¬b∨¬a∧c)∧(b∧c∨a∨b)=(a∨c)∧b
      

   Для упрощения использован пакет "Wolfram Mathematica":
   
   Simplify[a && b || ! (a && ! b || ! a && c) && (! b && c || a || b)]
   
   (a || ! c) && b
   
   

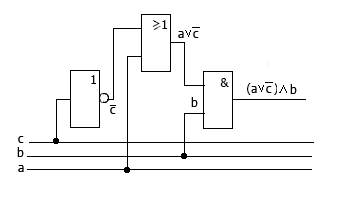
   Электрическая схема, соответствующая полученной функции: