Логические задачи
1. На трех клоунах Баме, Биме и Боме рубашки и туфли трех цветов: красном, синем, зеленом. На Биме и туфли, и рубашка одного цвета. На Боме нет ничего красного. Туфли Бама были зеленые, а рубашка нет. Какого цвета были рубашки и туфли на каждом из трех клоунов?
РЕШЕНИЕ:
Составим таблицу:
|
 |
Туфли на Боме не красные и не зеленые, т.е синие. Тогда туфли на Биме красные и рубашка тоже красная. Рубашка Бама не может быть ни зеленой, ни красной, т.е. она синяя. Рубашка Бома — зеленая.
|
|
|||||||||||||
| Бом Бим ;\ Бам |
2. Пять отпускников встретились как-то в клубе и завели разговор, кто где живёт.
-
— Амели: - Я живу в Акапулько, как и Бенуа, а Пьер живёт в Париже.
-
— Бенуа: - Я живу в Бресте, Шарль - тоже. Пьер живет в Париже.
-
— Пьер: - Я, как и Амели не живу во Франции; Мелани живет в Мадриде.
— Мелани:- Мой отец живёт в Акапулько, мать в Париже, а я живу в Брюсселе.
— Шарль: -Амели приехала из Акапулько, Бенуа - тоже. Я сам живу в Брюсселе.
Заметим, что каждый из отпускников два раза сказал правду и один раз солгал. Кто где живет?
РЕШЕНИЕ:
Предположим, что Пьер не живет в Париже, тогда Амели и Бенуа (из утверждения Амели, где есть две правды и одна ложь) живут в Акапулько. Однако, из утверждения Бенуа (где есть две правды и одна ложь) следует, что если Пьер не живет в Париже, то он (Бенуа) живет в Бресте, что противоречит условию.
Предположим, что Пьер живет в Париже и утверждение Амели, о том что Бенуа живет в Акапулько - ложь. Тогда Амели живет в Акапулько, Пьер живет в Париже, Бенуа не живет в Акапулько.
Тогда из утверждения Бенуа правда, что он живет в Бресте, а Пьер - в Париже, ложь, что Шарль живет в Бресте.
Акапулько не во Франции - в Мексике. Пьер говорит правду, что Амели живет не во Франции, лжет, что он не живет во Франции и говорит правду о Мелани. Мелани живет в Мадриде. Мелани врет, что она живет в Брюсселе. Она живет в Мадриде. Её отец действительно живет в Акапулько, а мать - в Париже. Тогда Шарль говорит правду об Амели и о себе.
Шарль живет в Брюсселе. Шарль врет о Бенуа, тот не приехал из Акапулько. Бенуа живет в Бресте.
Итак,
| ♦ | Амели живет в Акапулько | |
 |
| ♦ | Бенуа живет в Бресте | |
 |
| ♦ | Пьер живет в Париже | |
 |
| ♦ | Мелани живет в Мадриде | |
 |
| ♦ | Шарль живет в Брюсселе | |
 |
3. Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной.
Сколько шестиклассников:
- Являются читателями обеих библиотек;
- Не являются читателями районной библиотеки;
- Не являются читателями школьной библиотеки;
- Являются читателями только районной библиотеки;
- Являются читателями только школьной библиотеки?
Заметим, что первый вопрос является ключевым для понимания и решения данной задачи. Ведь не сразу сообразишь, как получается 20 + 25 = 45 из 35. В первом вопросе звучит подсказка к пониманию условия: есть ученики, которые посещают обе библиотеки. А если условие задачи изобразить на схеме, то ответ на первый вопрос становится очевидным.
РЕШЕНИЕ:
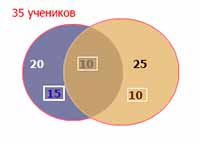
- 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.
- 35 – 20 = 15 (человек) – не являются читателями районной библиотеки. (На схеме левая часть левого круга)
- 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки. (На схеме правая часть правого круга)
- 35 – 25 = 10 (человек) – являются читателями только районной библиотеки. (На схеме правая часть правого круга)
- 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки. (На схеме левая часть левого круга).
Очевидно, что 2 и 5, а также 3 и 4 – равнозначны и ответы на них совпадают.
При решении данной задачи мы использовали способ ее графического представления при помощи так называемых кругов Эйлера. Этот способ был предложен Леонардом Эйлером и широко используется при решении логических задач.
 |
 |
| Л.Эйлер | Дж. Венн |
Леонард Эйлер (1707, Базель, Швейцария – 1783, Санкт-Петербург, Российская империя) – математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.
Английский математик, логик, философ Джон Венн (1834 - 1923) в какой-то мере улучшил идею Эйлера, поэтому
иногда применяют диаграммы Венна-Эйлера или просто диаграммы Венна.
4. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят лилии, а пятеро — фиалки. И только у двоих есть и лилии и фиалки. Cколько у меня подруг? Всего 4+2+3=9
Круги Эйлера можно применить для иллюстрации утверждений общего характера, что отображено на рисунке.
 |
Все А есть В |  |
Все А есть В, и все В есть А |
 |
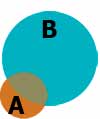Некоторые А есть В |  |
Ни одно А не есть В |
5. Несколько заддач, для решения которых можно применять круги Эйлера.
- Некоторые пальмы являются ромашками. Все ромашки громко кричат. Следовательно, все пальмы громко кричат. Неверно.
- Все бабочки плавают на спине. Все журавли являются бабочками. Следовательно, все журавли умеют плавать на спине. Верно
- Некоторые кроты являются ботинками. Некоторые ботинки плохо танцуют. Следовательно, некоторые кроты плохо танцуют. Неверно
- Два созвездия никогда не бывают похожи друг на друга. Окна и двери выглядят совершенно одинаково. Следовательно, окна и двери не являются двумя созвездиями. Верно
- Никого из слонов не берут в космонавты. Все люди – слоны. Следовательно, никто из них не пойдет в космонавты. Верно
Квантор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и созд.ающих высказывание. Чаще всего упоминают:
- Квантор всеобщности (обозначение: ∀, читается: «для любого…», «для каждого…», «для всех…» или «каждый…», «любой…», «все…»).
- Квантор существования (обозначение: ∃, читается: «существует…» или «найдётся…»)
Выражение (∀x∈X)P(x) читается так:
- для любого (всякого, каждого) значения x из X P(x) истинно;
- всякий (любой, каждый) элемент x множества X (где X — множество значений переменной x) обладает свойством P(x);
- каково бы ни было x, P(x) истинно.
Выражение (∃x∈X)P(x) читается так:
- существует значение x из X такое, что P(x) истинно;
- по крайней мере для некоторых x, принадлежащих X, P(x) истинно;
- существует элемент x множества X, обладающий свойством P(x);
- по крайней мере (хотя бы) один элемент x множества X обладает свойством P(x);
- некоторые элементы множества X обладает свойством P(x);
- найдётся такое x из X, что P(x) истинно.
Обозначим P(x) предикат «x делится на 5». Используя квантор всеобщности
(∀x∈ℕ)P(x),
можно формально записать следующие высказывания (конечно, ложные):
- любое натуральное число кратно 5;
- каждое натуральное число кратно 5;
- все натуральные числа кратны 5;
Следующие (уже истинные) высказывания используют квантор существования
(∃x∈ℕ)P(x):
- существуют натуральные числа, кратные 5;
- найдётся натуральное число, кратное 5;
- хотя бы одно натуральное число кратно 5.
Формула включений и исключений
Пусть задано конечное множество А. Число его элементов обозначим m(А). Найдем сколько элементов содержится в множестве А ∪ В. Основная формула нахождения числа элементов суммы двух множеств
m(А ∪ В) = m(А) + m(В) – m(А ∩ В) (1)
Действительно, m(А ∪ В) — это сумма числа элементов множеств А и В, но при подсчете элементы, принадлежащие А ∩ В учитывались дважды. С помощью формулы (1) можно получить формулы для определения числа элементов суммы любого числа множеств. Например,
m(А∪В∪С)=m(А∪(В∪С))=m(А)+m(В∪С)- -m(А∩(В∪С))= =m(А)+m(В)+m(С)-m(В∩С)-m((А∩В)∪(А∩С))= =m(А)+m(В)+m(С)-m(В∩С)-(m(А∩В)+m(А∩С)- -m((А∩В)∩(А∩С)))= =m(А)+m(В)+m(С)-m(В∩С)-m(А∩В)-m(А∩C)+ +m(А∩В∩С)
m(А∩В∩С)=m(А)+m(В)+m(С)-m(А∩В)-m(В∩С)- -m(А∩C)+m(А∩В∩С) (2)
Формулы (1) и (2) называют формулами включений и исключений.
6. Из 100 школьников английский знают 42, немецкий — 30, французский — 28, английский и немецкий — 5, английский и французский — 10, немецкий и французский — 8, английский, немецкий и французский — 3 школьника. Сколько школьникоpв не знают ни одного языка? Задачу можно решить с помощью диаграммы Эйлера
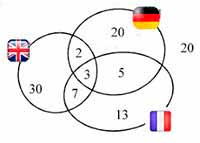
- Так как 3 языка знают 3 школьника,
- то английский и немецкий знают 5 – 3 = 2,
- английский и французский — 10 – 3 = 7,
- немецкий и французский — 8 – 3 = 5 школьников.
- Только английский знают 42 –(2 + 3 + 7) = 30,
- только немецкий — 30 – (2 + 3 + 5) = 20,
- только французский — 28 – (3 + 5 + 7) = 13 школьников.
- Ни одного языка не знают 100 – (2 + 3 + 5 + 7 + 13 + 20 + 30) = 20 школьников.
С применением метода «включений и исключений» эта задача решается так:
Обозначим через А — множество школьников, знающих английский язык; N — множество школьников, знающих немецкий язык; F — множество школьников, знающих французский язык.
Тогда m(A) = 42, m(N) = 30, m(F) = 28, m(A ∩ N) = 5,
m(A ∩ F) = 10, m(N ∩ F) = 8, m(A ∩ N ∩ F) = 3.Найдем с помощью формулы включений и исключений количество школьников, знающих хотя бы один из перечисленных иностранных языков.
m(A ∪ N ∪ F) = m(A) + m(N) + m(F) - - m(A ∩ N) – m(A ∩ F) – m(N ∩ F) + m(A ∩ N ∩ F) = = 42 + 30 + 28 – 5 – 10 – 8 + 3 = 80.
Следовательно, не знают ни одного иностранного языка:
100 – 80 = 20 школьников.
7. Задача автора «Алисы в Cтране чудес» Льюиса Кэррола. Во время средневековой страшной битвы 85% сражавшихся потеряли ухо, 80% - глаз, 75% - руку, 70% - ногу. Каков минимально возможный процент участников битвы, которые одновременно лишились уха, глаза, руки и ноги?
Запишем это так: m(U)=85 m(G)=80 m(R)=75 m(N)=70.
- Не лишиились уха — 15%
- Не лишиились глаза — 20%
- Не лишиились руки — 25%
- Не лишиились ноги — 30%
Тогда, лишились какого либо органа или не лишились ничего 15+20+25+30=90%. Лишились уха, глаза, руки и ноги 100-90=10%
Логика занимает достойное место в математическом образовании многих стран. К сожалению, Россия, по целому ряду прчин отстает. В качестве примера приведем несколько задач из психометрического экзамена, проводившегося в Израиле в последние годы. Этот экзамен является аналогом нашего ЕГЭ, его сдача обязательна при поступлении в ВУЗ.
Психометрический вступительный экзамен проводится Израильским центром экзаменов и оценок (ИЦЭО). При поступлении в большинство ВУЗов удельный вес психометрии примерно равен удельному весу аттестата зрелости. Результаты экзамена действительны в течение 7 лет со дня проведения экзамена. Участвовать в экзамене можно неограниченное количество раз, однако минимальный промежуток времени между экзаменами составляет около 6 месяцев. Для подсчета вступительного балла ВУЗы используют наивысшую из всех действительных оценок.
Экзамен составлен из тестов, включающих в себя вопросы множественного выбора (англ. Multiple choice) по трем направлениям: словесное (вербальное) мышление, количественное мышление (математические способности) и английский язык.
С 2012 года экзамен включает в себя написание эссе на заданную тему, оценка за эссе включается в оценку за словесное мышление. Некоторые ВУЗы принимают во внимание оценки за каждое из направлений в отдельности. Суммарная оценка выставляется по шкале от 200 до 800 баллов. Психометрический экзамен проводится на нескольких языках: иврите, русском, арабском, французском и испанском.
8. В рамках программы повышения эффективности работы фирмы ее директор решил уволить несколько сотрудников. Когда оставшиеся сотрудники фирмы выразили свое недовольство. он ответил им: «Лес рубят. щепки летят». директор сравнил:
- уволенных сотрудников с лесом
- оставшихся в фирме сотрудников со щепками
- процесс повышения эффективности с вырубкой леса
- увольнение соотруднниковв с вырубкой леса
9. Сочетание четырех следующих утверждений создает противоречие.
Устранение какого из этих утверждений сохранит данное противоречие в силе?
- Гена старше Ромы.
- Гена младше Сережи и Ольги.
- Сережа старше Ольги.
- Ольга младше Ромы.
10. В некотором жилом доме проживают только рыжеволосые и блондины.
Известно. что:
- Рыжеволосым могут нравиться только те люди, которым не нравится ни один рыжеволосый.
- Блондинам могут нравиться только те люди, которые не нравятся ни одному рыжеволосому.
- Утверждение: Макс и Мориц. которые проживают в этом здании, нравятся друг другу.
Отсюда следует, что —
- они оба — рыжеволосые
- они оба — блондины
- один из них рыжеволосый, а другой — блондин
- описанная выше ситуация невозожна.
11. Найдите лишнюю фигуру:
Ответы: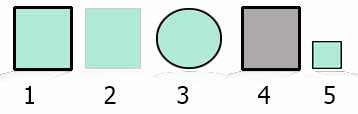
Задача Ответ 8 3 9 3 10 3 11 1 - содержит только одно отличие
от любой дргой фигуры. Все остальные
фигуры попарно имеют более одного отличия
