Untitled

Логические функции

Логическая переменнная (boolean) — переменная, которая может принимать только два значения True, False — Правда, Ложь — 1,0.

Логическая функция от n логических переменных x1, x2, …, xn – это функция, которая может принимать только два значения 1 или 0 (True-False, Истина-Ложь).

В классической (двузначной) логике «истина» и «ложь» называются истинностными значениями высказываний.

Предполагается, что других значений, характеризующих степень уверенности в справедливости информации (вероятно, возможно и прочее), высказывания приниматьне могут. Первые многозначные логики были построены независим друг от друга польским ученым-логиком Я. Лукасевичем в 1920 году и американским ученым-логиком Э. Постом в 1921 году. С тех пор построены и исследованы десятки и сотни таких логик.


Ян Лукасевич 1878-1956	Эмиль Леон Пост 1897-1954

Каждая переменная может принимать только два значения. Следовательно имеется 2ⁿ возможных комбинаций n переменных.

Логическая функция будет определена, если известно ее значение для каждой из 2ⁿ возможных комбинаций. Она может быть представлена с помощью соответствующей таблицы истинности. Логическую функцию можно задать аналитически, с помощью таблицы истинности или с помощью электрической схемы.

Рассмотрим, например функцию трех переменных f(x,y,z). Функция f(x,y,z) будет определена, если будут заданы ее значения (0 или 1) для каждой из восьми комбинаций в таблице:

N	x	y	z
0	0	0	0
1	0	0	1
2	0	1	0
3	0	1	1
4	1	0	0
5	1	0	1
6	1	1	0
7	1	1	1

ЗАМЕЧАНИЯ:

В последнем столбце таблицы должны быть значения функции f, пока они не проставлены.
В строках таблицы x,y,z двоичные цифры записи числа номера строки, например для 5 101. первая строка всегда одни 0, последняя 1.
В последнем столбце 0 и 1 чередуются через строку, потом через две, — через 4 и т.д.

Следует отметить, что имеется 2^N способов присвоить значения 0 или 1 функции для N комбинаций переменных. Поскольку N=2n, то, следовательно,2^2ⁿ существует различных функций n переменных.

Логические функции одной переменной

Существует 4 логических функции одной переменной. Обозначим эти 4 функции как f0 — f3. Значение индекса функции равно значению ее двоичного представления в соответствующей колонке таблицы истинности:

x	f0	f1	f2	f3
0	0	1	0	1
1	0	1	1	0

Функции f0 и f3 – это константные функции, равные нулю и единице независимо от значения аргумента x и называются они: тождественный ноль и тождественная единица соответственно, эти функции называют конституанты 0 и 1 соответственно Функция f2 противоположна значению аргумента: f2(x) = ¬x=x . Эту функцию называют «инверсия», «отрицание» или же функция НЕ (NOT).

Логические функции двух переменных

Имеется 2^2ⁿ =16 логических функций двух переменных. Определения этих функций, обозначенные от f0 до f15, даны в нижеследующей таблице.

N	x	y	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
1	0	1	0	0	1	1	0	1	1	0	0	0	0	1	1	1	1
2	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
3	1	1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

Функции f0 и f15 – конституанты 0 и 1 соответственно.
Функция f3 не зависит от y и равна x (f3(x,y) = x).
Функция f5 не зависит от x и равна y (f5(x,y) = y).
Функция f10 не зависит от x и является отрицанием переменной y (f10(x,y) = ¬y ).
Функция f12 не зависит от y и является отрицанием переменной x (f12(x,y) = ¬x ).
Оставшиеся функции являются функциями, непосредственно зависящими от двух переменных x и y. Среди них можно выделить наиболее часто употребляемые функции f1 и f7.
Функция f1 принимает истинное значение (значение 1), если и только если оба аргумента одновременно являются истинными (x=1 и y=1). Ее называют «конъюнкция», или же «функция логического умножения», или же «функция И » и обозначают обычно как f(x,y) = xy=x &y=x^;y.
Функция f7 принимает значение 1 , если хотя бы один из аргументов x = 1 или y = 1. Ее называют «дизъюнкция», или же «функция логического сложения», или же «функция ИЛИ (OR)» и обозначают обычно как
f7(x,y) = x ∨ y или x || y, или x+y.
Функция f6(x,y) = x ⊕ y.
Это функция «исключающее ИЛИ (XOR)» (f6(x,y) = 1, если x = 1 или y = 1, но не одновременно). Еще ее называют «сумма по модулю 2», или же «функция несовпадения». Операция, которая соответствует этой функции, часто обозначается в виде x ⊕ y.
Функция f9(x,y) = x ≡ y.
Это функция «логической идентичности» или же «функция совпадения». (f9(x,y) = 1, если x и y имеют одинаковые значения). Ее иногда обозначают как x ≡ y или x ∼ y или x ↔ y. '
Функция f8(x,y) =x ↓ y.
Это «функция НИ» (f8(x,y) = 1, если ни x ни y не равны 1), или же функция «стрелка Пирса», обозначаемая иногда как f8(x,y)=x ↓ y. '
Функция f14(x,y) = x | y.
Это функция «логической несовместимости» (f14(x,y) = 1, если x и y одновременно не равны 1), или же функция «штрих Шеффера», обозначаемая иногда как x | y . '
Функция f2(x,y) = Она называется «функция запрешения» (f2(x,y) = 1, если x = 1 и y = 0), иногда обозначаемая как '
Функция f4(x,y) = Она называется «функция запрещения» (f4(x,y) = 1, если x = 0 и y = 1), иногда обозначаемая как


Чарльз Сандерс Пирс 1839-1914		Генри Морис Шеффер 1882-1964

Функция f11(x,y) = x →y Это функция «импликаци» (f11(x,y) = 1 для всех комбинаций аргументов, кроме x = 0 и y = 1}.

Функция f13(x,y) = y → x Это функция «вовлечения» или «следования» (f13(x,y) = 1 для всех комбинаций аргументов, кроме x = 1 и y = 0).

Основные операции булевой алгебры

Булева алгебра — раздел математики, изучающий логические выражения и операции. Логические выражения представляют собой высказывания — некоторые утверждения, которым всегда можно сопоставить одно из двух логических значений:истина или ложь (их можно обозначать как True и False, 1 и 0 ).

Для сравнения, элементарная алгебра занимается арифметическими выражениями и операциями.

Булева алгебра получила свое название в честь своего создателя Джорджа Буля (1854 г.), являющегося одним из предтеч математической логики.

Среди своих прочих приложений, булева алгебра позволяет программистам формулировать сложные условия для применения в условных операторах или операторах цикла, а компьютерам—определять их истинность или ложность, вычисляя соответствующую информацию на основе определенных правил.

На практике определяют некоторое число основных операций, с помощью которых можно описать все остальные операции. Такие операции называются функционально полным набором. Среди всех наборов обычно выделяют один, состоящий из трех операций: логическая инверсия, логическое сложение и логическое умножение.

Операция инверсии

Это унарная операция, для нее небоходима только одна переменная. Другое наззвание - отрицание, НЕ, NOT.

Результат операции инверсии обозначают ¬x добавляя черту над переменной x . Таблица истинности этой функции имеет следующий вид:

x	y
0	1
1	0

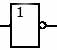
На структурных схемах данную логическую функцию обозначают с помощью следующего символа:

Логическое сложение

Операция логического сложения (дизъюнкция), соответствующая функции ИЛИ (OR), является бинарной операцией и выдает в качестве результата значение, называемое логической суммой.

В выражениях для этой операции приняты следующие обозначения f= x ∨ y=x+1.

Таблица истинности этой операции имеет вид:

x	y	f
0	0	0
1	0	1
0	1	1
1	1	1

На схемах эта функция обозначается с помощью символа

Логическое умножение

Логическое умножение (конъюнкция) соответствует функции И (AND) и выдает в качестве результата значение, называемое логическим произведением. В выражениях для этой операции приняты следующие обозначения: x ∧ y , или x · y , или же . Таблица истинности этой операции имеет вид:

x	y	f
0	0	0
1	0	0
0	1	0
1	1	1

На схемах эта функция обозначается с помощью символa:

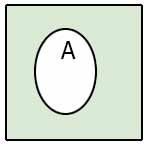
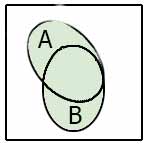
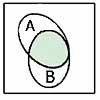
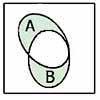
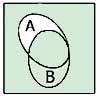
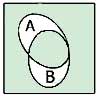
Применение диаграмм Венна

Дмаграммы Венна для некоторых логических функций

A	A ∨ B	A ∧ B

A ⊕ B	A → B	A ≡B

Логическая операция — в программировании операция над выражениями логического (булевского) типа, соответствующая некоторой операции над высказываниями в алгебре логики. Как и высказывания, логические выражения могут принимать одно из двух истинностных значений — «истинно» или «ложно». Логические операции служат для получения сложных логических выражений из более простых. В свою очередь, логические выражения обычно используются как условия для управления последовательностью выполнения программы.

В некоторых языках программирования (например, в языке Си) вместо логического типа или одновременно с ним используются числовые типы. В этом случае считается, что отличное от нуля значение соответствует логической истине, а ноль — логической лжи.

Значение отдельного бита также можно рассматривать как логическое, если считать, что 1 означает «истинно», а 0 — «ложно». Это позволяет применять логические операции к отдельным битам, к битовым векторам покомпонентно и к числам в двоичном представлении поразрядно. Такое одновременное применение логической операции к последовательности битов осуществляется с помощью побитовых логических операций. Побитовые логические операции используются для оперирования отдельными битами или группами битов, применяются для наложения битовых масок, выполнения различных арифметических вычислений.

Среди логических операций наиболее известны конъюнкция (AND), дизъюнкция (|OR), отрицание (NOT). В языке программирования BASIC применяются операции исключающее ИЛИ (XOR), импликация (IMP) и эквивалентность (EQV).

Обычное применение логических опрааций в программировании опратор условного перехода или оператор выбора if.

Рассмотрим несколько примеров.

На вход программы вводится натуральное число 1≤n<99 . На выходе программы нужно напечатать это число и слово « рубль», «рубля», «рублей» в соотетствии с нормами рускогог языка. Например, 21 рубль, 56 рублей, 64 рубля.
Решение
```
s="Рублей";
rr=Mod[n,10];    /* остаток от деленя на 
                      10, последняя  цифра n */
If[aa==1 &&n!=11,s="Рубль"];   
                   /* && - and != не равно  */
If[aa>=2 &&aa<=4,s="Рубля" ];
Print[n,"  ",s];
```
.
На вход программы подаются два числа (x, y) - координаты точки на плоскости. На выходе нужно напечатать "Да" или "Нет" - попадает точка в закрашенную область

1 2

Решение 1.
```
If[x^2+y^2<=1 &&x>0&&y>x^2, Print["Да"],
      Print["Нет"];
```
Решение 2.
```
If[x^2+y^2<=1 &&x y>0&&Abs[y]>Abs[x]-1,
 Print["Да"],
  Print["Нет"];
```

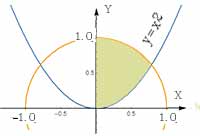
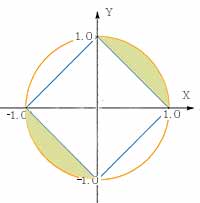
Точка должна попасть внутрь окружности с центром в начале коордират и радиусом 1. Уравнение окружности x^2+y^2=1. Попадание внутрь окружности определяется условием: x^2+y^2<1.

В задаче 1 ромб на графике определен уравнением |x|+|y|=1, координаты точки, помещенной вне ромба должны отвечать условию |y|>|x|-1

ОНЛАйН КУРС

ОСНОВЫ
МАТЕМАТИЧЕСКОЙ
ЛОГИКИ